There is now widespread awareness of the space debris problem amongst policymakers, scientists, engineers and the public. Thanks to pivotal work by J.C. Liou and Nicholas Johnson in 2006 we now understand that the continued growth of the debris population is likely in the future even if all launch activity is halted. The reason for this sustained growth, and for the concern of many satellite operators who are forced to act to protect their assets, are collisions that are expected to occur between objects – satellites and rocket stages – already in orbit. In spite of several commentators warning that these collisions are just the start of a collision cascade that will render access to low Earth orbit all but impossible – a process commonly referred to as the ‘Kessler Syndrome’ after the debris scientist Donald Kessler – the reality is not likely to be on the scale of these predictions or the events depicted in the film Gravity. Indeed, results presented by the Inter-Agency Space Debris Coordination Committee (IADC) at the Sixth European Conference on Space Debris show an expected increase in the debris population of only 30% after 200 years with continued launch activity.
Collisions are still predicted to occur, but this is far from the catastrophic scenario feared by some. Constraining the population increase to a modest level can be achieved, the IADC suggested, through widespread and good compliance with existing space debris mitigation guidelines, especially those relating to passivation (whereby all sources of stored energy on a satellite are depleted at the end of its mission) and post-mission disposal, such as de-orbiting the satellite or re-orbiting it to a graveyard orbit. Nevertheless, the anticipated growth of the debris population in spite of these robust efforts merits the investigation of additional measures to address the debris threat, according to the IADC.
On the face of it, there appears to be considerable procrastination or, worse, apathy towards the development of guidelines for debris removal in spite of calls for action. But is this really the case?
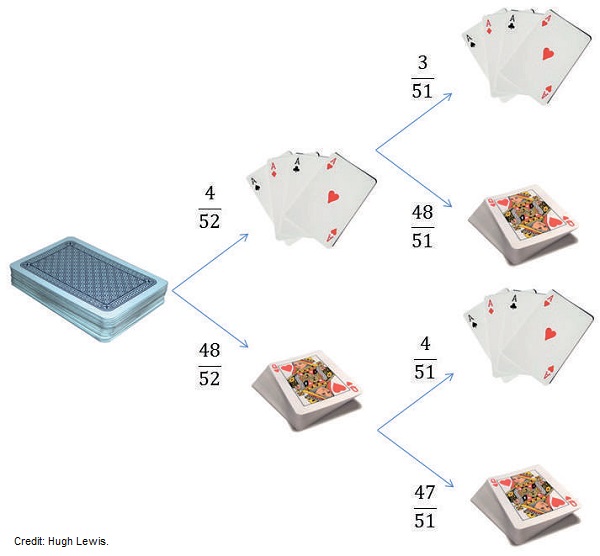 This probability tree shows the possible outcomes from drawing two cards from a pack of 52 regular playing cards. It can be used to illustrate the difficulties accociated with the choice of which piece of space junk to remove.
This probability tree shows the possible outcomes from drawing two cards from a pack of 52 regular playing cards. It can be used to illustrate the difficulties accociated with the choice of which piece of space junk to remove.
No progress?
In the nine years following the publication of the work by Liou and Johnson there has been considerable interest shown in remediation of the space environment. In particular, significant effort has been invested across the globe in the development of methods to remove objects from low Earth orbit. The European Space Agency, for example, recently announced its intention to seek ministerial approval for a mission to deorbit a European spacecraft in the next decade. The Agency has conducted numerous studies to investigate appropriate and reliable methods to achieve this. A key driver for these widespread efforts has come from the work conducted using computer codes – evolutionary models – of the debris environment, which suggest that the growth of the debris population can be prevented if particular spacecraft or rocket stages are removed. In the computer simulations, these objects are identified as the most likely to collide and so the consequence of their removal in reality should be a reduction in the number of collisions that will occur in the environment, which would curb the generation of new fragmentation debris.
Given that is has been nearly a decade since the publication of the work by Liou and Johnson, it is surprising to some that no guidelines have yet been introduced at the international or national level, which detail the remediation measures that can be taken by government and industry. In fact, a recent announcement by NASA of a focus on technology development rather than in-flight demonstrations of debris removal technologies was greeted with some criticism. On the face of it, there appears to be considerable procrastination or, worse, apathy towards the development of plans or guidelines for debris removal in spite of calls for action. But is this really the case?
The real issue comes from the seemingly simple task of identifying the correct debris to remove from orbit …
In fact, the situation is not as simple as it might appear; there are some fundamental questions that remain to be answered about debris removal. Of particular concern are issues relating to ownership, liability and transparency. Many of the technologies that have been put forward for debris removal could also be used to remove or disable an active spacecraft, for example. Hence, it can be argued that these technologies could be used as weapons. There are also questions about the cost of a sustained programme of debris removal – some engineers put it at tens of trillions of dollars.
However, perhaps the most important reason for the lack of relevant guidelines is that we don’t yet know how to accomplish remediation, by which we mean cleaning up space, in practice. That is not to say that we don’t know what technologies we might need. As mentioned above, there has been considerable effort already expended towards understanding these requirements and moving the necessary technology forwards.
For one-off use, some technologies are very nearly ready. The real issue comes from the seemingly simple task of identifying the correct debris to remove from orbit. Until we can solve this problem, the likelihood is that debris remediation will not succeed, the debris population will continue to grow – seemingly out of our control – and the attempt will come at great cost. Without the reasonable expectation of success, it is virtually impossible to define appropriate and robust guidelines that can be used to direct remediation endeavours.
Playing the debris game
To understand the difficulty associated with the apparently simple task of identifying debris to remove, we can use the analogy of a game involving a pack of 52 regular playing cards. In this analogy each card represents an object in the space environment that we might want to remove to prevent a collision from occurring. After shuffling the cards, we place each one face down, separately, on a table. Our objective now is to try to identify the aces and to remove them from the table, as these particular cards represent satellites or other large debris objects that will be involved in collision at some point in the future. We can remove from the table as many cards as we want, but each time we remove one we have to pay $10. In addition, we are not allowed to look at the card once it has been removed (if a satellite is removed from orbit there is no way to determine with certainty that it would have been involved in a collision). Finally, we have to pay $100 for every ace that is left on the table, which represents the potential losses arising from collisions involving our satellites (in reality, the cost to replace a satellite could be between $100,000 and $2 billion).
 Earth’s orbits will inevitably fill with more and more space debris between 2009 (top) and 2209 (below).
Earth’s orbits will inevitably fill with more and more space debris between 2009 (top) and 2209 (below).
How should we approach this problem? The back of the cards are identical, so clearly there is no way to determine where the aces are and the only way to be certain that we have removed all of the aces is to remove all of the cards from the table. In our example, this would cost the maximum of $520. In the space environment, we have exactly the same problem: we don’t know with certainty which objects might be involved in a collision and it is too costly to remove them all, so we are forced to choose. Let’s assume that we choose to remove one card at a cost of $10, what is the probability that we have removed an ace? The probability of an ace is four divided by 52; in other words about 0.08 or 8%. Thus the probability that the card is not the ace of spades is 1-0.08, or 92%. It is far more likely that the card is not an ace and that our $10 has been spent for no gain.
 No matter what we do, space debris is going to increase. This simulation concentrates on the years 2009 (left) to 2209 (right) and concentrates on low Earth orbits.
No matter what we do, space debris is going to increase. This simulation concentrates on the years 2009 (left) to 2209 (right) and concentrates on low Earth orbits.
What happens if we now take a second card (which will cost us another $10)? Well, the probability that the second card is an ace will depend on whether the first card was an ace. If it was, then the probability that the second card is also an ace is three divided by 51 (because there are now only three aces remaining in the pack, which has been depleted by one card). If the first card was not an ace, then the probability that the second card is an ace is four divided by 51 (because there are still four aces in the depleted pack). Figure 1 shows all of these possible outcomes and their probabilities in the form of a tree.
We can use this probability tree to determine the probability that we have removed both of the aces. There is only one path through the tree where this is an outcome, and we simply multiply the probabilities indicated on each branch to find the answer: 4/52 multiplied by 3/51 which gives us a probability of about 0.0045, or 0.45%, at a cost of $20 for two cards removed. Not very encouraging!
However, we can also determine the probability that we have removed AT LEAST one of the aces. We do this in a slightly counter-intuitive way: we look at the branches of the tree where we did not remove any of the aces (again, there is only one path through the tree where this is an outcome) and follow the same procedure as before by multiplying the probabilities on each branch. This gives us 48/52 multiplied by 47/51, which is about 0.85 or 85% chance that we did not remove any of the aces. In other words, there is a 15% chance that we successfully removed at least one of the aces. This is a more encouraging, but these are still not very good odds!
It turns out that we need to remove more than nine cards (at a cost of $90) to have a better than even chance that we have removed at least one of the aces, or more than 22 cards (at a cost of $220) if we want to be 90% sure that we have removed one of the aces. Even if we are successful, there could be three more aces still left on the table, so we would still have to pay $520 in total, which – coincidentally – is what we would have paid if we had chosen to remove all of the cards.
Real world troubles
Moving from our analogy back to the space environment, the situation is more troubling. Of the approximately 20,000 objects in orbit and currently being tracked by the US Space Surveillance Network, about 6% of them are objects with masses greater than one tonne that have some chance of being involved in a collision and that we might want to consider removing. The trouble with the card game analogy is that all of the cards are identical and the probability that one is the ace of spades is the same as the probability that another is the ace. There is no way to identify the best cards to remove from the table.
In reality, our chances of preventing a collision are much better than the card game suggests because some objects are more likely than others to be involved in a collision and we can focus our attention on these. For example, objects in heavily populated orbits, such as Sun-synchronous orbits at altitudes 600–900km, are more likely to be involved in a collision because of the congestion there. If we target these objects (and others in similarly congested orbits) and make use of predictions of their collision probability to guide us, then it turns out that we only need to remove about 50 objects on average to reduce the number of catastrophic collisions by one, according to results from studies by space agency members of the IADC.
…trying to predict collisions that might take place in five days, or in 50 days or more, is like trying to predict the weather five days ahead, or 50 days ahead.
There are still collisions because there are still many large objects that we left in-orbit but the odds have improved in our favour. Nevertheless, even if multiple objects could be targeted for removal by one “cleaner” spacecraft (and five targets seem to be a common choice), many missions – often complicated and demanding – must be conducted just to prevent one collision.
Why can’t we do a better job of predicting collisions and remove only those objects we know for certain will be involved? Well, trying to predict collisions that might take place in five days, or in 50 days or more, is like trying to predict the weather five days ahead, or 50 days ahead. There are many parameters that can affect the trajectory of a satellite, including the orientation of the satellite, whether it is tumbling, and space weather (which can affect the amount of drag experienced by satellites). Even small errors in the initial values of these can lead to large discrepancies in predictions of the position of satellites, compared with the reality, even after a relatively short period of time. This affects our collision probability predictions. In fact, we take the same approach as weather forecasters: we use models to generate the probability of particular outcomes, but these outcomes are not certain, and never will be.
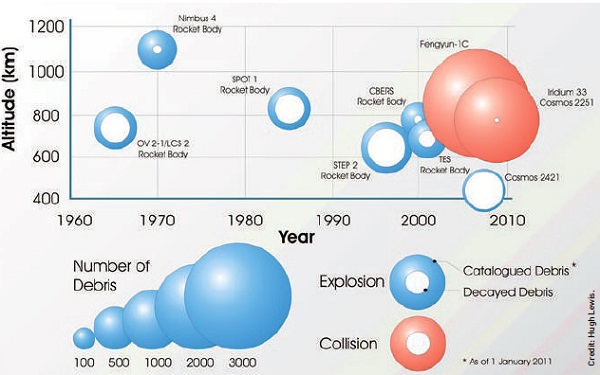 There have been a number of key fragmentation events, either from explosions or collisions, that have significantly increased the space debris problem.
There have been a number of key fragmentation events, either from explosions or collisions, that have significantly increased the space debris problem.
So, we are left with technologies that can be employed to remove debris on a case-by-case basis, which is the approach adopted by ESA with their planned e.Deorbit mission, but there are still challenges that need to be overcome in identifying the best targets for removals. This problem must be solved before the necessary direction and guidance can be provided to those interested in mounting a sustained programme of removals, which is required for effective remediation of the space debris environment.
Guidance, in terms of particular targets, their number, mission requirements and constraints, is important for increasing the likelihood that remediation efforts will be effective and worthwhile. For such guidance to emerge, we need to reconsider our unreasonable expectation of certainty.
Hugh Lewis is a Senior Lecturer in Aerospace Engineering at the University of Southampton. He is also a member of the UK Space Agency delegation to the Inter-Agency Space Debris Coordination Committee and a member of the UK delegation to the United Nations Committee on the Peaceful Uses of Outer Space.














