Currently, there is no single global standard for the calendar year. In space, none of the geocentric, terrestrial analogue calendars used today (of which there are about 40) makes practical sense. For strategic purposes, celestial navigation and astrodynamics, they are effectively useless. In an attempt to rectify the situation, the space nation of Asgardia – which was formed in October 20167 – has developed an astrocentric, fixed-standard, 13-month reference calendar.
The Asgardia calendar is focused on the 88 major constellations listed in the catalogue of bright stars, of which 13 zodiacal constellations are on the ecliptic. The calendar is based on atomic clocks and is designed to indicate a single time in all possible spacecraft, including the Earth as one such ‘equipotential spacecraft’. This article describes the basic strategic principles of the astrocentric fixed 13-month reference zodiac calendar of the space state of Asgardia.
The issue of the reform of the geocentric analogue Gregorian calendar began to be actively discussed in the 19th century, when its logical shortcomings were revealed. However, all attempts to optimise the calendar, to reform it and, in particular, to produce the correct fixed form, have so far been unsuccessful.
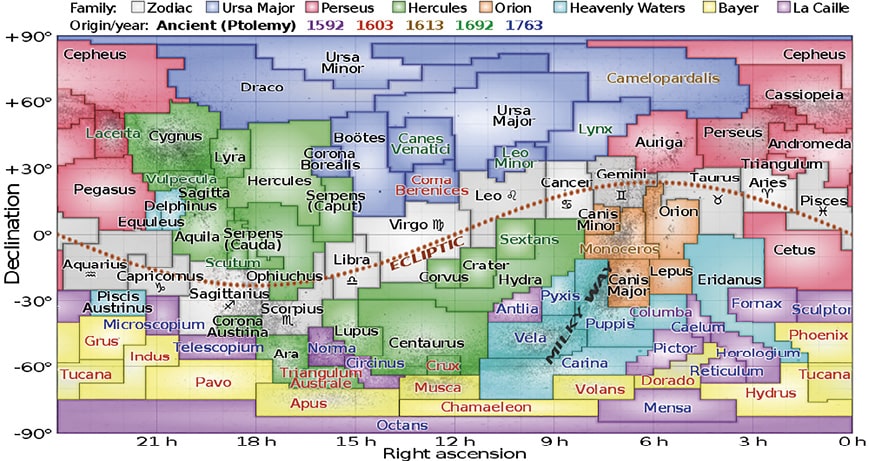The eighty-eight constellations officially recognised by the International Astronomical Union (IAU).
The exceptional complexity of the issue and a large number of failures led scientists to conclude that the task was impossible, even theoretically. This was because the astronomically certain length of the solar (tropical) year in days cannot be expressed as a multiple of seven, or even an integer, in order to make a universal calendar that is suitable for each and every year. And this is why a single, 13-month reference calendar has been proposed by the author on behalf of the space state of Asgardia. It is based on a strict digital mathematical model and is not associated with conventional, geocentric analogue models of the Earth’s motion around the Sun.
In space, none of the geocentric, terrestrial-analogue calendars used today (of which there are about 40) makes practical sense
The annual cycle of the star Sirius was of particular importance in Ancient Egypt. The priests of the time noticed that the star is clearly visible in the northern hemisphere at the latitude of Memphis, but for 70 days is visible only in the southern hemisphere. Its next appearance in the northern hemisphere after 70 days of absence was accurately predictable and the annual cycle was given the scientific name of the “heliacal year of the star Sirius”.
This is relevant because the tropical year of the Sun - a period of time equal to the time between two successive solstices in the tropic of Cancer or Capricorn - is calculated from the heliacal year of the star Sirius [see Box 1: tropical year of the Sun calculation].
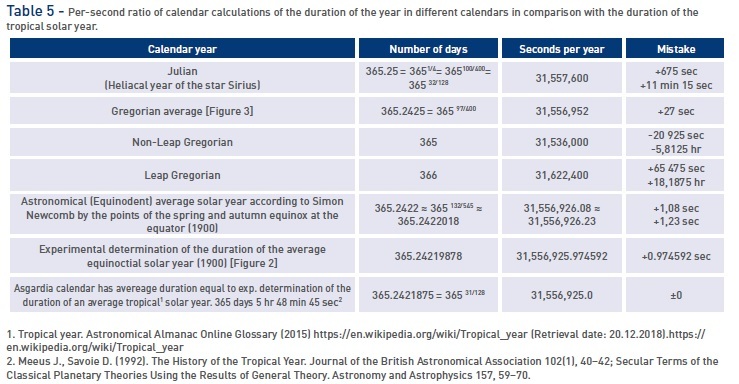
In 46BC, the heliacal calendar of the star Sirius was moved from Egypt to Rome by Gaius Julius Caesar. However, the seasonal tropical year of the Sun (365 [31/128] = 365.2421875 days) was 1/128 of a day shorter than the heliacal year of Sirius, as discovered for the first time in 325AD at the Council of Nicaea. The result was that the estimated date of the spring equinox in the calendar was moved three days, from March 24 in 46BC to March 21 in 325AD: [46 + 325]/128 = [371]/128 = 2.898 ≈3 days. This requires a ‘solar’ correction of [1/128] days to give 365.2421875 days: 365 [32/128] days — [1/128] days = 365 [31/128] days = 365.2421875 days.
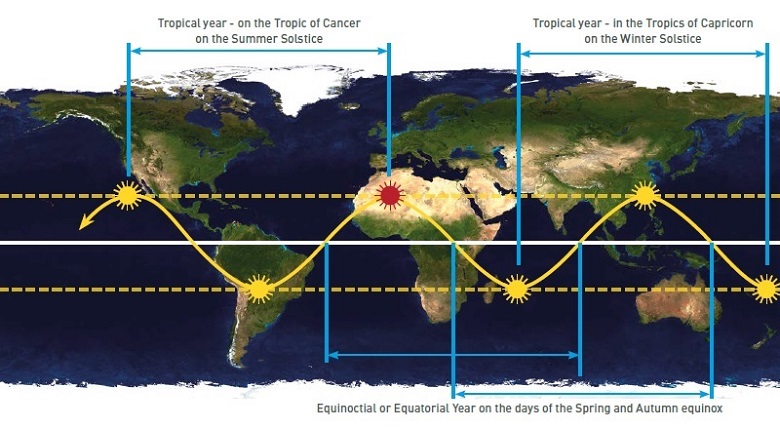Determination of the duration of the solar year.
Following the correction in the cycle of 128 years of the solar tropical year, there were 31 leap years and 97 non-leap years (31 + 97 = 128 years), instead of 32 leap years and 96 non-leap years in the basic calculation of the Julian calendar of the heliacal year of the star Sirius.
Thus, the accuracy of the calculated tropical calendar after correction is regulated by ‘plug in leap years’ with a frequency of 31/128 = 0.2421875 days (that is, 5 hours 48 minutes 45 seconds, or 20,925 seconds). The correction has a perfect averaged accuracy, in that the error of the calculated tropical calendar in relation to the real tropical astronomical year after the mathematical correction procedure is on average zero [see Box 2: solar calendar accuracy].
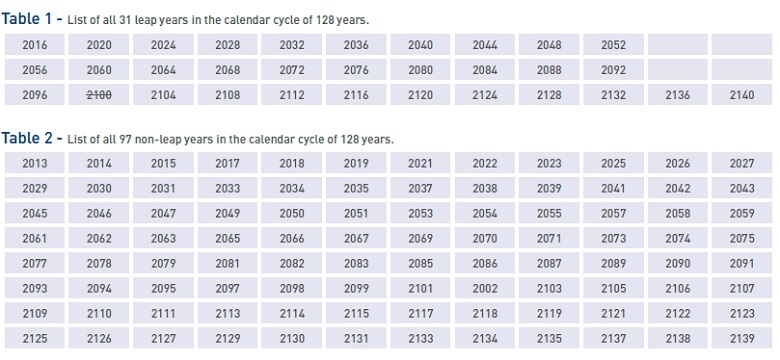
The list of all leap years (31 years, listed in Table 1) is given in the 128-year cycle (2012 + 128 = 2140), in which just three days will be attributed to the new year holidays: the 29th and the 30th day of Capricorn and the 1st day of Aquarius. For all these leap years, the same leap matrix will be used.
The ideal core of the standard 13-month reference calendar consists of 364 days
Table 2 shows all non-leap years (97 years) in the 128-year cycle (2012 + 128 = 2140). For all these 97 non-leap years, the same non-leap matrix will be used. In the non-leap year, two days will be attributed to the new year holidays: the 29th day of Capricorn and the first day of Aquarius. Leap year 2100 was moved to the group of non-leap years to comply with the leap calendar correction with a frequency of 31/128 = 0.2421875 days (that is, 5 hours 48 minutes 45 seconds, or 20,925 seconds).
Architecture of standard calendar
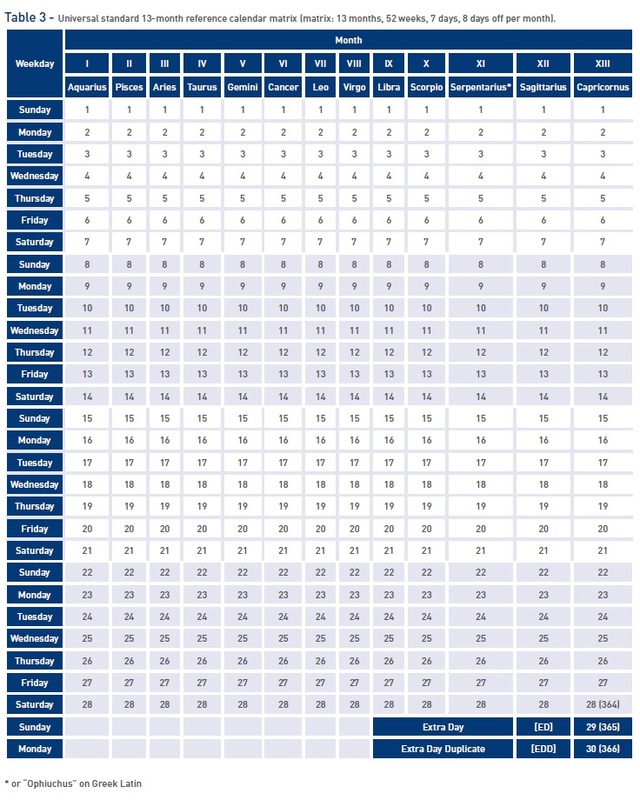
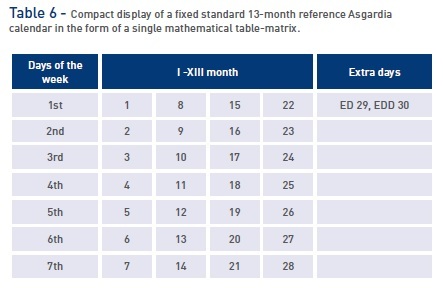
The ideal core of the standard 13-month reference calendar consists of 364 days: 52 weeks of 7 days each (Table 3). Each of the 13 months have the conventional names of the ecliptic zodiac constellations and contains exactly 28 days: (I) Aquarius; (II) Pisces; (III) Aries; (IV) Taurus; (V) Gemini; (VI) Cancer; (VII) Leo; (VIII) Virgo; (IX) Libra; (X) Scorpio; (XI) [Serpentarius, Ophiuchus or Apheuhus] (Asgard [Ásgard in Scandinavian mythology - heavenly city, abode of the gods] or Horus, one of the most important Egyptian gods or Ashur, the name of the main God of Assyria); (XII) Sagittarius; (XIII) Capricornus.
Each of the four quarters contains exactly 91 days. In a normal year, there are 365 days (including ED - Extra Day). In a leap year, there is an additional 366th day (EDD - Extra Day Duplicate). The name EDD has alternative names: LD (Leap Day) and BD (Bisextile Day or the same Leap Day).
After each additional 365th day in a normal year and after each additional 366th day in a leap year, the calendar matrix returns to its original state, back to the beginning of the year (Morozov`s principle of active synchronisation of the real year with the ideal year).
Therefore, each new year always begins with the first day of Aquarius, Sunday. We consider the calendar as a mathematical digital time counter. From Table 4, it follows that the days of the week in the traditional calendars (in the bottom row of each cell of the calendar matrix) are mobile: at the beginning of each ordinary year they are shifted one day of the week forward, and the beginning of each year, following the leap year, is shifted immediately two days of the week forward with the immutability and constancy of the numerical series relative to each other.
In all modern calendars, the opposite is true: the constant is the grid of days of the week, and the variable is the shift of numerical series relative to each other — one day in a normal year and two days in the next after leap year. In astronomical terms (but not in economic terms) this transformation is completely equivalent in relative parameters (Morozov`s principle of calendar equivalence). It is necessary to choose between either variable series of numbers at a constant grid of days of the week or constant (fixed) series of numbers at a variable grid of days of the week.
The constant rows of calendar days with a variable grid of days of the week (in the lower, current, scale of the calendar matrix) has an important advantage in economic terms over the constant grid of days of the week and variable rows of numbers adopted today in all terrestrial calendars.
Leap Years: making up for lost time
Economic effect of standard calendar
In the Asgardia calendar, each new year always starts on the same date and on the same day of the weekLeap
In the Asgardia calendar, each new year always starts on the same date and on the same day of the week. It allows one to have the same universal day all over the world (the top row in each cell of the calendar matrix), which saves tens of thousands of tonnes of paper, dyes, printing and transportation costs.
With constant (fixed) rows of numbers in the calendar matrix of the permanent calendar and with a variable grid of days of the week at the bottom of the current scale of the permanent calendar, the dates of events will always remain identical: this includes holidays, dates of launch windows into space, schedules in schools and universities, parliaments, network schedules, stock and bank calculations, etc. They will remain fixed from year to year and will not require, as is the case now, any annual recalculations.
The upper universal (absolute) series of numbers of the calendar matrix in each cell never changes. This makes it possible to bring to a single mathematical denominator any specific calendar system placed in the second (lower) row of each cell of the calendar matrix (Table 4). For each cycle of 128 years, only two types of calendar are used: leap and non-leap, which differ only in the number of days related to the new year (three days in a leap year and two days in a non-leap year). In all other respects, the calendars are absolutely identical.
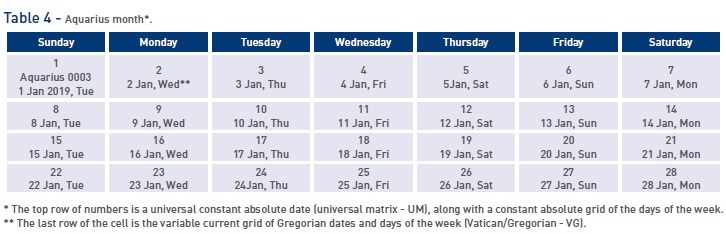
In the proposed calendar, the numerical axis of history is divided into uniform cycles of the same type (128 years each) and contains two rows of numbers: the upper universal and the lower Gregorian (VG). The date is recorded in two ways: universal (UM) and ordinary, according to the Gregorian calendar. For example, 1 Aquarius 0003, Sunday (UM) / 1 January 2019, Tuesday (VG).
Industrialisation strategy
The calendar is intended to ensure international cooperation in the strategy for the industrialisation of space
The strategy for the industrialisation of space today naturally follows the era of capitalist and socialist industrialisation strategies on Earth, but is expected to lead to the gradual replacement of terrestrial attributes currently extended to space. In particular, this will involve the replacement of the terrestrial calendar system with a space-based one.
The calendar of the space state of Asgardia is a fixed-standard, digital reference, uniform version of the 13-month global space calendar of the sixth strategic socio-economic formation of human civilisation, the first stage of which was marked by the creation of the state of Asgardia on 12 October 2016 in Paris.
The calendar itself was implemented by Igor Raufovich Ashurbeyli, Head of state of Asgardia, Decree No. 2 from 1 January 2017 and approved by the Parliament of Asgardia dated: Virgo 13, 0003 //July 28, 2019. The calendar is intended to ensure international cooperation in the strategy for the industrialisation of space. The standard 13-month reference calendar of the space state of Asgardia is a purely civil neutral calendar for the first time in the history of civilization. It does not serve any religious groupd or political parties. It is designed to serve the purely economic tasks of the new space society, the new space socio-economic formation.
About the author
Sergei Lvovich Morozov studied at the Medical Institute and graduated from the University of Izhevsk in 1976. He also graduated from the Moscow Research X-ray Radiological Institute of the Ministry of Health of the Russian Federation in Moscow in 1985, from the Finance Academy under the Government of Russia in 2002, and completed doctoral studies in Central Economics and Mathematics at the Russian Academy of Sciences in 2016. Morozov has been the chairman of the board of Elbimbank (1990-2000), adviser to the Secretary General of the EurAsian Economic Community (2005-2008), a senior research fellow at the National Development Institute of the Russian Academy of Sciences (2017) and a Member of the first Parliament of Asgardia (2018).
